Minggu, September 27, 2009
Contoh Membangkitkan Data dari Beberapa Distribusi dengan Bahasa Pemrograman PASCAL
0 komentar Diposting oleh benaz_poenya di 06.45Sumber : Tugas Kuliah Teknik Simulasi
Pada materi teknik simulasi dalam posting sebelumnya telah dijelaskan bahwa cara membangkitkan data untuk menerapkan percobaan simulasi dapat dilakukan dengan menggunakan 2 program, yaitu program Minitab dan bahasa pemrograman Pascal. Dalam posting sebelumnya, untuk mendapatkan bangkitan data telah dilakukan dengan menggunakan program Minitab. Maka, pada posting kali ini akan dibahas mengenai contoh membangkitkan data dengan menggunakan bahasa pemrograman Pascal. Bangkitan data yang akan dibahas adalah data yang dibangkitkan dari beberapa distribusi.
Distribusi Uniform
Contoh hasil akhir setelah program dijalankan (run) :
Distribusi Eksponensial
Contoh hasil akhir setelah program dijalankan (run) :
Distribusi Bernoulli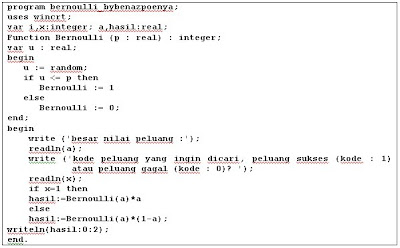
Contoh hasil akhir setelah program dijalankan (run) :
Distribusi Log Normal
 Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Label: simulasi
Pemeriksaan dan Pengujian pada Keacakan Data beserta Distribusi-nya
0 komentar Diposting oleh benaz_poenya di 05.00Sumber : Catatan Kuliah Teknik Simulasi (Kamis, 17 September 2009).
Untuk membuat suatu simulasi dari suatu kasus, biasanya diperlukan bangkitan data dari suatu distribusi berdasarkan gambaran distribusi dalam kasus tersebut. Misal, kasus dalam antrian yang cenderung membentuk grafik distribusi eksponensial. Oleh karena itu, untuk dapat mengetahui apakah bangkitan data yang telah didapatkan sudah sesuai distribusi perlu dilakukan suatu pengujian dan pemeriksaan pada data tersebut.
Pemeriksaan
Pemeriksaan dilakukan hanya berdasarkan visual saja. Atau dengan kata lain, dilihat dengan menggunakan bantuan plot (tidak perlu melibatkan statistik uji). Karena hanya dilihat berdasarkan visual maka kesimpulan yang nantinya diperoleh pasti akan berbeda antara satu orang dengan orang yang lain.
Plot yang digunakan (pada program Minitab) dalam pemeriksaan biasanya adalah Histogram, Stem-and-Leaf, ataupun Scatterplot. Namun, tidak menutup kemungkinan untuk dapat melakukan pemeriksaan dengan menggunakan plot yang lainnya. Misal, dengan menggunakan PiQi PLOT.
PiQi PLOT dapat dibuat dengan 2 program, yaitu program Minitab ataupun dalam bahasa pemrograman Pascal.
Algoritma dalam pembuatan PiQi Plot adalah sebagai berikut :
1. Memulai perintah pemrograman.
2. Mengurutkan data bangkitan sehingga menjadi :
3. Menentukan nilai Pi.
4. Menentukan nilai Qi sedemikian hingga 
5. Membuat scatterplot antara nilai Qi dengan X(1).
6. Perintah pemrograman selesai.
Jika dibuat dengan menggunakan program Minitab (setelah bangkitan data didapatkan) dapat dilakukan dengan menggunakan perintah seperti di bawah ini :
[ Keterangan: Karena nilai Pi merupakan cdf. Sedangkan nilai Pi adalah invers dari nilai Qi. Maka, jika diketahui nilai Pi, nilai Qi dapat dicari melalui invers cdf (invcdf) ]
Maka, dari perintah pemrograman tersebut akan didapatkan grafik :

Pengujian
Pengujian dilakukan dengan melibatkan statistik uji. Statistik uji yang dimaksud tersebut meliputi H0, H1, dan kesimpulan. Kesimpulan dapat dilihat berdasarkan nilai p-value. Jika nilai p-value <> alfa maka kesimpulan yang didapat adalah gagal tolak H0. Pengujian biasanya dilakukan setelah pemeriksaan. Karena dalam pemeriksaan akan didapatkan kesimpulan yang berbeda satu sama lain maka melalui pengujian, kesimpulan yang didapatkan akan sama.
Cara melakukan pengujian dapat dilakukan dengan berbagai cara. Namun, yang biasanya digunakan adalah Run Test dan Kolmogorov-Smirnov Test. Kedua pengujian ini juga dapat dibuat dengan menggunakan 2 program, yaitu program Minitab ataupun dalam bahasa pemrograman Pascal.
Untuk melakukan Run Test pada program Minitab, perintah yang dituliskan adalah :
[ Keterangan: Kolom C1 merupakan kolom data bangkitan yang telah didapatkan ]
Dan untuk melakukan Kolmogorov-Smirnov Test pada program Minitab dapat dituliskan dengan menggunakan perintah seperti di bawah ini :
[ Keterangan: Nilai Pi merupakan distribusi yang bersifat empiris karena dihitung berdasarkan data, sedangkan nilai Qi merupakan distribusi yang bersifat teoritis karena dihitung berdasarkan H0. Hasil yang nantinya didapatkan dari Kolmogorov-Smirnov Test ini akan cenderung berdistribusi Uniform karena beda jarak antara distribusi yang bersifat empiris dan teoritis dekat ]
Selain, menggunakan kedua pengujian tersebut dapat juga menggunakan pengujian yang lain seperti Uji Keselarasan (Chi-Square).
Teori :
 Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Label: simulasi
Minggu, September 13, 2009
hmmmm...kemaren lage iseng pengen ngubek2 kamar...sekalian melakukan inspeksi barang2 sampah..hahahaha..eh, ga tau nyah nemuin cerpen bikinan dewe waktu jaman SMA..hohoho...pikir2 lage...knapa ga coba di share di blog??? meskipun blog ini tercipta tanpa sengaja gara2 tugas Teknik Simulasi (tapi ternyata bikin blog menyenangkan juga..pantesan sahabat2quw mulai sahabat SMA ampe kuliah keranjingan nge-blog)...
cerpen ini cuman cerpen sederhana dan amatir..jadi terucap kata maap jika banyak kekurangan. jika ada kesamaan nama, karakter, atau cerita jelas bukan atas unsur kesengajaan..
Tangan itu kini sudah tak seperti dulu lagi. Tangan itu kini tak lebih dari tulang kering yang hanya terbungkus kulit yang semakin keriput. Tangan yang dulu sering membelaiku sebelum tidur, mengusap air mataku saat aku tak bisa bersikap sebagai laki-laki jantan sewaktu berkelahi dengan teman-temanku, dan tangan yang sering menyuapiku makan saat aku sedang terbaring sakit. Dan setiap kali mataku memandang sosok tua yang lemah dan tak berdaya itu sedang terbaring di pembaringan yang hanya beralaskan seprai tipis, rasanya aku tak sanggup bertahan hidup di dunia ini. Ingin rasanya aku menggantikan penderitaannya yang tak kunjung berakhir. Penyakit yang sampai sekarang dianggap aib oleh semua orang itu telah mengambil senyum ibuku yang dulu sering kulihat. Ibuku positif mengidap penyakit AIDS. Penyakit itu datang tanpa pernah kusangka sebelumnya. Ibuku tertular penyakit yang hingga sekarang belum ada obatnya itu setelah mendonorkan darah di rumah sakit terpencil di kotaku. Jarum yang digunakan adalah jarum bekas yang tidak disterilkan terlebih dahulu. Ingin rasanya aku marah pada pihak rumah sakit atau pada orang yang telah tega menularkan penyakit mematikan ini pada ibuku, namun tiap kali kuutarakan niatku ini pada ibuku, tiap kali itulah aku hanya mendapat senyuman dan jawaban yang singkat agar aku bersikap lebih dewasa dan lebih sabar. Aku iri pada ketabahan yang ditunjukkan ibuku. Aku malu sebagai laki-laki mengapa aku tak bisa bersikap seperti bapak yang bisa membimbing ibu sebelum bapak meninggal dunia. Sebagai gantinya justru ibulah yang selalu membimbingku hingga aku dewasa.
Kupegang sekali lagi tangan tua itu. Kupastikan ibu sudah terlelap. Lalu aku mulai beranjak dari tempat tidurnya dan mulai memasuki kamarku. Malam ini aku sulit sekali untuk memejamkan mata. Aku masih teringat permintaan ibu yang sering diutarakannya padaku, katanya itu adalah permintaan ibu yang terakhir sebelum ibu meninggal dunia. Tak pernah kubayangkan bagaimana hidupku tanpa sosok ibu di sampingku. Tapi permintaan itulah yang sering mengusikku akhir-akhir ini. Permintaan sederhana dari seorang ibu. Ibu ingin melihatku menikah. Sebenarnya permintaan itu bagiku tidaklah sulit. Aku sudah mempunyai calon. Dia adalah anak dari seorang kyai di kampungku. Aisyah, namanya. Wanita sederhana yang mempunyai senyum termanis yang pernah kulihat serta berbagai akhlak terpuji. Dan masalah menikah sering disinggung berulang kali oleh ayah Aisyah, Kyai Slamet. Beliau ingin aku segera melamar Aisyah sehingga aku dan Aisyah tak akan terjerumus terlalu jauh pada lembah dosa yang bernama pacaran. Tapi keadaanlah yang selama ini melarangku untuk tidak bertindak gegabah. Semua orang di kampungku tak pernah tau bahwa ibuku mengidap AIDS. Mereka semua hanya tahu kalau ibuku sakit parah. Jika aku melamar Aisyah, tentu saja Aisyah beserta keluarganya akan tahu kondisi ibuku yang sebenarnya. Dan aku pasti akan malu setengah mati. Harga diri seorang laki-lak sepertiku pasti akan tercoreng. Mereka pasti akan berpikiran jelek tentang ibuku. Rasanya aku belum kuat untuk menghadapi itu.
Adzan subuh kudengar sayup-sayup dari surau di sebelah bukit. Aku beranjak bangun dan kumulai sholat untuk menenangkan batinku serta mengucap syukur pada Allah. Setelah sholat, aku menengok ibuku serta membawakan baskom berisi air untuk wudhu. Seperti biasanya ibuku sholat dalam keadaan terbaring di dipan kecilnya. Tubuhnya benar-benar tak bisa digerakkan. Erangan-erangan itu masih saja kudengar. Tiap kali kudengar erangan itu tiap malam, tiap kali itulah aku meneteskan air mata seraya mengucapkan asma Allah dalam hati agar aku diberi kesabaran dan ketenangan batin.
Sebelum aku berangkat kerja, ibu masih sempat mengucapkan permintaan terakhirnya lagi padaku. Dan seperti sebelum-sebelumnya aku hanya mengucapkan insya Allah dan kucium keningnya sambil mengucapkan salam. Dalam perjalanan, pikiranku mulai berkecamuk tak karuan. Sampai kerja pun aku benar-benar tak bisa konsentrasi. Di satu sisi, aku ingin melaksanakan permintaan terakhir ibuku, namun di sisi lainnya aku benar-benar merasa malu atas kondisi ibu, apa kata orang nanti. Lalu apakah Kyai Slamet mau menerima kalau aku adalah anak dari seorang ibu pengidap AIDS, apakah Aisyah juga mau menerima aku sebagai suaminya. Aku belum siap dan aku belum rela jika aku harus melihat reaksi keluarga Aisyah yang akan menolakku. Tapi, tak ada jalan lain aku harus mencoba, tak ada satu orang pun yang tahu kapan usia ibu akan berakhir dan aku tak mau membuatnya kecewa. Jika ini adalah jalan satu-satunya yang harus kutempuh maka aku rela menempuhnya asal aku bisa melihat senyum cerah ibu seperti dulu lagi. Aku segera membuat keputusan, selepas pulang kerja aku akan segera mengunjungi rumah Aisyah guna membicarakan ini.
Tanganku masih saja mengeluarkan keringat. Aku benar-benar tegang. Melihat Kyai Slamet di hadapanku seperti ini rasanya berat untuk memulai suatu pembicaraan. Namun, wajah Kyai Slamet masih saja sabar menunggu kata-kataku yang sudah ada di ujung lidah. Kubaca bismillah dalam hati dan mulai kuutarakan permasalahan yang mengganjal dalam hatiku. Selesai bicara, kuhembuskan nafas mencoba mengatur gejolak di dalam dadaku meskipun itu tidak banyak membantu sama sekali. Kupandangi wajah Kyai Slamet diam-diam. Nampaknya beliau sedang berpikir. Kulihat mulutnya terbuka, kutunggu kata-kata yang akan muncul. Tapi mulut itu tertutup lagi. Lama kutunggu jawaban yang akan dilontarkan, namun jawaban itu tak kunjung muncul jua. Pupuslah sudah harapan-harapanku. Kubayangkan wajah ibuku yang tak akan tersenyum lagi.
Selama perjalanan pulang ke rumah, aku ingin segera menemui ibuku. Mencium tangannya dan memohon restunya. Ya, ternyata lamaran yang sudah kuajukan diterima. Kyai Slamet memintaku untuk datang kembali bersama ibu dan beberapa keluarga besarku yang sudah tinggal sedikit untuk melamar Aisyah secara resmi. Kubuka pintu depan tanpa mengucap salam. Langsung saja aku lari menuju kamar ibuku. Kali ini aku pasti akan melihat senyum yang sudah bertahun-tahun tak pernah kulihat lagi. Senyum itu pasti akan menghiasi wajah ibuku. Kubuka pintu kamarnya. Kulihat mata ibu terpejam. Rupanya ibu sedang tidur, mungkin juga sedang mimpi indah karena kulihat senyum samar di bibirnya. Kudekati ibu dan kucium keningnya. Dingin. Kening ibu sangat dingin. Kupegang tangan, kaki, semuanya dingin. Tak terasa air mataku mulai membasahi wajah ibu. Aku menangis seperti dulu lagi saat aku kalah dalam berkelahi semasa kecil. Bedanya kali ini tak ada lagi tangan lembut yang mengusap air mataku.
Innalillahi wainaillahi roji'un. Ya Allah, semoga Kau menerima arwah ibu yang paling aku sayangi ini di sisi-Mu. Semoga Kau mengampuni segala dosa-dosanya dan menjauhkannya dari api neraka. Semoga saja Engkau memberi kami kesempatan sekali lagi untuk berkumpul di barisan Rasulullah kelak dan senyum ibu dapat kulihat lagi. Amiinn Ya Robbal Alamin...
-Cerita ini dibuat untuk memperingati Hari Ibu-
December'06
benernya masi banyak cerpen yang dulu sempat tercipta karena banyak waktu luang..tapi banyak juga yang udah hilang ga tau arahnya hehehe...seandainya aq menemukan lagi cerpen2 itu dan seandainya juga aq punya banyak waktu luang (pluz Internet tersedia) Insya Allah aq posting lagi..
banyak kelemahan dalam cerpen ini jadi yang berniat ngasih komen dan kritik yang membangun monggo...
Sabtu, September 12, 2009
Pembangkitan Bilangan Acak (PSEUDO-RANDOM GENERATION RANDOM NUMBERS)
0 komentar Diposting oleh benaz_poenya di 16.13Sumber : Catatan Kuliah Teknik Simulasi (Kamis, 10 September 2009).
Whereas random numbers were originally either manually or mechanically generated, by using such techniques as spinning wheels, or dice rolling, or card shuffling, the modern approach is to use a computer to successively generate pseudorandom numbers (Sheldon M.Ross, 2006).
Barisan bilangan random (acak) pada komputer dapat dihasilkan melalui suatu mekanisme (formula atau rumus) sehingga dapat diperkirakan bilangan random apa yang akan muncul. Hal inilah yang disebut bilangan random tidak betul-betul acak atau semu (dalam bahasa Inggris disebut Pseudo-random numbers).
Contoh :
Diketahui : a = 2 ; m = 5 ; X0 = 3
( Keterangan : Modulo adalah sisa pembagian dengan m. )
Pada hasil yang ditunjukkan di atas, dapat dilihat bahwa bilangan random yang muncul berulang. Agar tidak muncul berulang maka, nilai m yang diberikan harus berukuran sangat besar.
Ukuran besar suatu angka dalam komputer berbeda dengan ukuran besar pada bilangan desimal.
Jika pada bilangan desimal :
Bilangan desimal terbesar 1 digit adalah 9.
Bilangan desimal terbesar 2 digit adalah 99.
Bilangan desimal terbesar 3 digit adalah 999.
dan seterusnya.
Sedangkan pada komputer, bilangan desimal tidak dapat dibaca, yang dapat dibaca hanyalah bilangan biner. Pada komputer, bilangan biner terbesar adalah sebesar 32 digit. Apabila lebih besar dari 32 digit maka bilangan tersebut tidak akan terbaca oleh komputer.
Pada bilangan biner :
Bilangan biner terbesar 1 digit (1) adalah 1.
Bilangan biner terbesar 2 digit (11) adalah 3.
Bilangan biner terbesar 3 digit (111) adalah 7.
dan seterusnya.
Maka, apabila pada komputer bilangan biner terbesar yang terbaca adalah 32 digit maka besarnya adalah (perhitungan dilakukan dengan menggunakan rumus 2^k-1) 4.294.967.295.
Jadi, dapat diambil suatu kesimpulan bahwa untuk memunculkan suatu bilangan random dengan probabilitas perulangan (munculnya bilangan tersebut lagi) sekecil mungkin harus menggunakan ukuran nilai m yang sangat besar (pada komputer maksimal sebesar 32 digit bilangan biner)
ASAL-USUL BILANGAN RANDOM BERDISTRIBUSI UNIFORM (0,1)
Untuk membangkitkan data secara random pada distribusi Uniform (0,1) dapat dilakukan dengan menggunakan rumus seperti di bawah ini :
Where a and m are given positive integers, and where the above means that axn-1 is divided by m and the remainder is taken as the value of xn (Sheldon M.Ross, 2006).
Berdasarkan rumus di atas, maka simulasi untuk membangkitkan data bilangan random dengan distribusi yang lain dapat dilakukan.
Contoh :
1. Membangkitkan data bilangan random berdistribusi Uniform kontinyu x~μ(a,b) dengan menggunakan bahasa pemrograman Pascal adalah sebagai berikut :

2. Membangkitkan data bilangan random berdistribusi Eksponensial dengan menggunakan bahasa pemrograman Pascal adalah sebagai berikut :
Kedua contoh yang dipaparkan di atas dapat pula dilakukan dengan menggunakan bahasa pemrograman yang lain, misal dengan menggunakan software Minitab.
[Penjelasan membangkitkan data dengan menggunakan program Minitab telah dijelaskan pada contoh kedua dalam posting yang sebelumnya dengan judul Contoh Aplikasi Percobaan Simulasi]
Namun, untuk mengetahui apakah hasil bangkitan data dari Minitab benar atau tidak maka tetap diperlukan suatu pengujian. Pengujian ini dapat dilakukan dengan menggunakan Uji Autocorrelation (Otokorelasi).
Pengujian dengan menggunakan Uji Autocorrelation (Otokorelasi) pada program Minitab dilakukan seperti di bawah ini :
1. Membangkitkan data populasi sebanyak 1000 (Calc → Random Data → Uniform dengan lower endpoint (nilai minimum) sebesar 0 dan upper endpoint (nilai maksimum) sebesar 1).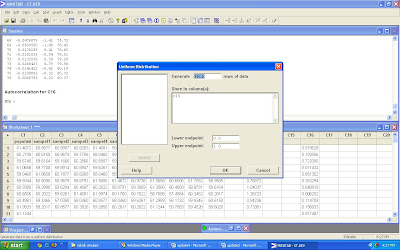
2. Melakukan pengujian dengan menggunakan Uji Autocorrelation ( Stat → Time Series → Autocorrelation)
Hasil akhir dari pengujian Autocorrelation tersebut adalah apabila data yang telah dibangkitkan berada melebihi garis merah maka data tersebut telah acak (random). Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Label: simulasi
Sumber : Buku Ajar Teknik Simulasi (Nur Iriawan)
Model simulasi diskrit digunakan untuk memodelkan suatu sistem yang berevolusi terhadap waktu sedemikian sehingga variabel state sistem hanya berubah nilai pada waktu-waktu tertentu yang banyaknya dapat dihitung. Contoh simulasi diskrit ini adalah antrian. Pada sistem antrian, secara analitis sistem antrian merupakan model yang mempunyai sifat kedatangan pelanggan ke dalam sistem dan kecepatan pelayanannya adalah menuruti distribusi Eksponensial. Sehingga, akan dengan mudah untuk menerapkan persamaan dan solusinya.
[Tambahan informasi : Sistem Antrian juga telah dibahas pada mata kuliah Riset Operasi]
MODEL ANTRIAN
Komponen pada sistem antrian : server (channel), clients (pelanggan), antrian.
Server (channel) : Single server atau Multiple server.
Antrian : Single antrian atau Multi antrian.
Parameter: tingkat distribusi kedatangan, waktu kedatangan, waktu pelayanan, panjang antrian, waktu tunggu, dan utilitas server (waktu sibuk atau total waktu).
Keterangan :
Clients (pelanggan) : individu-individu yang meminta jasa pelayanan.
Server (channel) : individu yang melayani individu yang lain yang meminta jasa pelayanan.
Parameter dalam antrian :
λ : rata-rata tingkat kedatangan.
w : rata-rata panjang antrian.
Tw : rata-rata waktu tunggu.
Ts : rata-rata waktu pelayanan.
Tq : rata-rata waktu yang dihabiskan di dalam sistem (Tw + Ts).
λmax : 1/Ts , tingkat maksimum (secara teori) yang dapat dilayani oleh sistem.
Notasi dalam antrian :
Notasi antrian yang sering digunakan pada sistem antrian satu tahap A/B/C : D/E/F
A menunjukkan sebagai distribusi waktu antar kedatangan.
B menunjukkan sebagai distribusi waktu pelayanan.
C menunjukkan sebagai banyaknya server.
D menunjukkan sebagai disiplin antrian.
E menunjukkan sebagai banyaknya kapasitas antrian.
F menunjukkan sebagai besar ukuran populasi.
Keterangan :
1. A dan B (distribusi kedatangan dan pelayanan pelanggan dalam sistem antrian).
M → Memoryless (Eksponensial / λ).
Er → Erlang (α,β).
G → Arbitrary waktu antar kedatangan.
D → deterministic arrivals or fixed length services.
Contoh : M/M/1 : FIFO/~/~
2. C (banyaknya server).
Menunjukkan banyaknya pelayan yang siap melayani pelanggan yang datang pada sistem antrian. Nilai C>1 menunjukkan bahwa server-server tersebut terpasang parallel.
3. D (disiplin antrian).
Disiplin antrian adalah cara server memilih pelanggan untuk dilayani. Terdapat beberapa pengembangan model dari disiplin antrian sebagai berikut :
(1) FIFO (First In First Out) atau FCFS (First Come First Serve).
Artinya, pelanggan yang pertama datang adalah pelanggan yang akan dilayani pertama kali.
(2) LIFO (Last In First Out) atau LCFS (Last Come First Serve).
Artinya, pelanggan yang terakhir datang adalah pelanggan yang akan dilayani pertama kali. Apabila menggunakan disiplin antrian ini maka akan mengakibatkan terjadinya penumpukan massa atau individu atau dengan kata lain akan tecipta suasana yang kacau.
(3) Random (acak).
Artinya, semua anggota populasi mempunyai peluang yang sama untuk terpilih. Populasi yang dimaksud ini adalah populasi individu yang akan dilayani. Hal yang sama akan terjadi seperti disiplin antrian sebelumnya apabila menggunakan disiplin antrian ini, suasana akan menjadi kacau.
(4) Prioritas.
Artinya, pelanggan yang pertama kali dilayani adalah pelanggan yang mempunyai prioritas terpenting. Hal ini biasanya terjadi pada UGD (Unit Gawat Darurat) pada suatu rumah sakit.
Jika pada suatu kasus, komponen D ini tidak dituliskan berarti disiplin antrian bernilai default (FIFO).
4. E (banyaknya kapasitas maksimum tempat antrian dalam sistem).
Komponen E dapat bernilai :
• Nol, jika tidak ada tempat antri yang disediakan.
• Satu, jika struktur antri hanya memberikan satu tempat antri.
• dst hingga tak terbatas.
Jika pada suatu kasus, komponen E tidak dituliskan berarti tempat antriannya tidak terbatas.
5. F (banyaknya pelanggan yang diijinkan untuk datang ke antrian.
Komponen F dapat bernilai :
• Terbatas, jika hanya pelanggan tertentu saja yang diperbolehkan datang ke dalam antrian.
• Tidak Terbatas, jika semua orang dengan keperluan sesuai tugas server, boleh datang ke antrian.
Jika komponen F ini tidak dituliskan, berarti semua orang dengan keperluan sesuai tugas server boleh datang ke antrian.


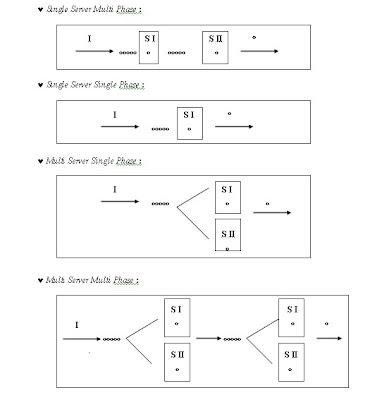
Untuk keterangan lebih lanjut pada sistem antrian server tunggal, dapat dijelaskan dengan menggunakan gambar di bawah ini :

Berdasarkan kasus di atas, terdapat 3 event (kejadian dalam sistem yang dapat mengubah state suatu sistem) :
1. Kedatangan konsumen (arrival) : merupakan event dikarenakan menyebabkan jumlah konsumen yang menunggu bertambah 1 state variabel.
2. Awal pelayanan konsumen : merupakan event dikarenakan menyebabkan status teller berubah dari idle menjadi busy dan jumlah konsumen yang menunggu berkurang 1 state variabel.
3. Kepergian konsumen (departure) : merupakan event dikarenakan menyebabkan status teller berubah dari busy menjadi idle dan jumlah konsumen yang menunggu berkurang 1 state variabel.
Keterangan :
a. Status teller digunakan untuk menentukan apakah konsumen yang baru datang harus menunggu atau bisa langsung dilayani.
b. Banyaknya konsumen yang sedang antri digunakan untuk menentukan apakah status teller setelah melayani konsumen menjadi idle atau tetap busy.
c. Waktu kedatangan tiap konsumen yang antri digunakan untuk menghitung waktu tunggu konsumen.
State Diagram M/M/1
State Diagram M/M/3
SIMULATION CLOCK
Karena model simulasi diskrit bersifat dinamis maka perlu untuk mencatat waktu-waktu tertentu sepanjang simulasi berlangsung dan butuh mekanisme untuk menaikkan waktu simulasi dari suatu nilai ke nilai lainnya. Variabel dalam model simulasi yang mencatat nilai waktu simulasi saat tertentu (current value of simulated time) disebut simulation clock.
Ada dua cara pendekatan yang digunakan untuk memajukan simulation clock, yaitu :
1. Pemajuan waktu berdasarkan event (next event time advance).
Simulation clock pertama kali diberi nilai 0 (nol) dan waktu-waktu terjadinya suatu event di masa mendatang ditetapkan. Nilai simulation clock diubah pada saat suatu event terjadi, setelah itu dilakukan perubahan nilai system state sesuai dengan event yang terjadi dan perubahan waktu terjadinya event berikutnya. Proses perubahan simulation clock dari satu event ke event lainnya berhenti sampe suatu kondisi yang telah ditentukan.
2. Pemajuan waktu dengan jarak tetap (fixed increment time advance).
Kenaikan nilai simulation clock adalah selalu dt (Δt), unit waktu. Setelah dilakukan update simulation clock, dilakukan pengecekan untuk menentukan apakah ada event yang terjadi selama interval waktu sebelumnya. Jika ya maka event yang terjadi dianggap terjadi pada akhir interval waktu, setelah itu system state (statistical counters) disesuaikan.
Metode pendekatan yang pertama lebih mudah dan lebih banyak digunakan pada mayoritas desain bahasa simulasi dan karena metoda yang kedua mempunyai banyak kelemahan. Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Label: simulasi
Sabtu, September 05, 2009
Sumber : Catatan kuliah Teknik Simulasi (Selasa, 1 September 2009).
Contoh percobaan simulasi secara sederhana dapat dijelaskan dengan menggunakan contoh kasus seperti di bawah ini :
Kasus Pertama :
Kasus Phi (π) adalah kasus dimana pelemparan kapur dilakukan pada sebuah papan tulis berbentuk segiempat yang di dalamnya terdapat lingkaran berukuran besar yang hampir memenuhi papan tulis tersebut.
Ilustrasi :
Pada setiap pelemparan kapur yang dilakukan mempunyai 3 kemungkinan yang akan terjadi :
1. Kapur yang dilempar akan jatuh di dalam lingkaran.
2. Kapur yang dilempar akan jatuh di luar lingkaran atau di dalam segiempat.
3. Kapur yang dilempar akan jatuh di luar segiempat.
Jika kapur yang dilempar tersebut, berada di daerah lingkaran (baik di luar ataupun di dalam) maka :
• Kapur berada di dalam lingkaran : x2+y2=1.
• Kapur berada di luar lingkaran : x2+y2<1.
Maka, simulasi berdasarkan kasus di atas dapat segera dirancang. Simulasi ini dapat dirancang dengan menggunakan aplikasi program komputer sesuai keinginan, misal dengan menggunakan bahasa Pascal atau dengan menggunakan bahasa Extend.
Di bawah ini, adalah simulasi yang dirancang dengan menggunakan bahasa Pascal. Sebelum bahasa Pascal dirancang maka terlebih dahulu disusun algoritma nya terlebih dahulu.
Algoritma untuk Kasus Phi :
1. Memulai perintah pemrograman.
2. Mendefinisikan i=0.
3. Mendefinisikan i=i+1, yang mempunyai arti bahwa percobaan simulasi yang akan dilakukan nanti dilakukan sampai ke-n percobaan.
4. Membangkitkan titik sebanyak 1000.
5. Mendefinisikan formula
6. Memberi syarat kondisi. Jika i<1000 maka kembali ke algoritma ke-3.
7. Mendefinisikan rumus
8. Menulis π.
9. Perintah pemrograman selesai.
Agar simulasi yang dirancang tidak menghasilkan hasil yang terlalu bervariasi maka percobaan dilakukan berulang-ulang hingga mendekati nilai yang sebenarnya. Artinya, dengan melakukan percobaan sebanyak n percobaan dan di setiap percobaan dihitung nilai pendekatan π ke n maka hasil yang diberikan akan tidak terlalu bervariasi.
Simulator dengan menggunakan bahasa pemrograman Pascal :
Apabila syntag tersebut dijalankan pada program Pascal maka hasil yang nantinya akan didapatkan adalah mendekati nilai sebesar 3.142.
Kasus Kedua :
Kasus Standard Deviasi adalah kasus yang dirancang untuk membandingkan standard deviasi populasi dengan standard deviasi sampel.
Statistik dapat digunakan untuk menduga parameter dari populasi. Statistik itu sendiri mempunyai sifat unbiased (tidak bias). Artinya, bahwa rata-rata yang diperoleh dari statistik dari keseluruhan sampel yang muncul harus sama dengan rata-rata yang diperoleh dengan parameter. Apabila statistik bersifat bias (tidak sama) maka hasil yang didapatkan terdapat selisih (bias). Contoh dari statistik yang bias adalah varians. Hal ini dapat dilihat dari pembagi rumus varians. Jika varians populasi pembagi nya adalah n, sedangkan pembagi varians sampel adalah n-1.
Sama dengan kasus pertama, sebelum merancang simulator terlebih dahulu menyusun skenario algoritma nya. Algoritma untuk Kasus Standard Deviasi adalah :
1. Memulai perintah pemrograman.
2. Membangkitkan data populasi secara random (acak) X ~ N (60,1) sebanyak 100.
3. Mengambil n sampel sebanyak 10.
4. Melakukan pengambilan sampel sebanyak 1000 kali.
5. Dari masing-masing populasi dan sampel, standard deviasi dihitung dengan menggunakan rumus di bawah ini : (S1 untuk standard deviasi populasi dan S2 untuk standard deviasi sampel).
6. Membandingkan hasil standard deviasi yang dihasilkan dari populasi dan sampel.
7. Perintah pemrograman selesai.
Pada kasus ini, simulator dirancang dengan menggunakan software komputer Minitab. Langkah-langkah merancang simulator :
1. Membangkitkan data populasi (Calc → Random Data → Normal dengan mean 60 dan standard deviasi 1).
2. Mengambil sampel dengan pengembalian sebanyak 10 (Calc → Random Data → Sample From Columns).
3. Menghitung standard deviasi dari populasi atau S1 kuadrat (Stat → Basic Statistics → Display Descriptive Statistics).
4. Menghitung standard deviasi dari sampel atau S2 kuadrat (Calc → Columns Statistics).
5. Membandingkan hasil S1 kuadrat dan S2 kuadrat.
Simulator dengan menggunakan software Minitab :
Hasil yang didapatkan dari perhitungan yang telah dilakukan dengan menggunakan program Minitab adalah :
1. Standard deviasi yang diperoleh dari populasi adalah sebesar 1.076.
2. Sedangkan, standard deviasi yang diperoleh dari sampel adalah sebesar :
0.86693
1.11470
1.00852
1.41006
1.17128
0.76872
1.04037
1.26723
0.94236
0.73381
Berdasarkan kedua hasil tersebut maka dapat diambil suatu kesimpulan bahwa standard deviasi dari populasi bias (ada selisih) dengan standard deviasi yang diperoleh dari sampel.
Oleh karena itu, percobaan ini diperlukan untuk dilakukan hingga ke n percobaan agar estimasi (pendugaan) nilai standard deviasi sampel bisa mendekati nilai standard deviasi yang diperoleh dari populasi.
Alasan kedua kasus di atas di ambil sebagai contoh aplikasi simulasi dikarenakan kedua kasus di atas sama-sama mempunyai hasil yang bervariasi jika tidak dilakukan hingga n percobaan. Sehinggga, dengan melakukan hingga n percobaan maka hasil yang kita dapatkan akan sesuai. Dan dari n percobaan itu juga akan diperoleh simulator yang baik. Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Label: simulasi




.jpg)


