Sabtu, September 12, 2009
Pembangkitan Bilangan Acak (PSEUDO-RANDOM GENERATION RANDOM NUMBERS)
Diposting oleh benaz_poenya di 16.13Sumber : Catatan Kuliah Teknik Simulasi (Kamis, 10 September 2009).
Whereas random numbers were originally either manually or mechanically generated, by using such techniques as spinning wheels, or dice rolling, or card shuffling, the modern approach is to use a computer to successively generate pseudorandom numbers (Sheldon M.Ross, 2006).
Barisan bilangan random (acak) pada komputer dapat dihasilkan melalui suatu mekanisme (formula atau rumus) sehingga dapat diperkirakan bilangan random apa yang akan muncul. Hal inilah yang disebut bilangan random tidak betul-betul acak atau semu (dalam bahasa Inggris disebut Pseudo-random numbers).
Contoh :
Diketahui : a = 2 ; m = 5 ; X0 = 3
( Keterangan : Modulo adalah sisa pembagian dengan m. )
Pada hasil yang ditunjukkan di atas, dapat dilihat bahwa bilangan random yang muncul berulang. Agar tidak muncul berulang maka, nilai m yang diberikan harus berukuran sangat besar.
Ukuran besar suatu angka dalam komputer berbeda dengan ukuran besar pada bilangan desimal.
Jika pada bilangan desimal :
Bilangan desimal terbesar 1 digit adalah 9.
Bilangan desimal terbesar 2 digit adalah 99.
Bilangan desimal terbesar 3 digit adalah 999.
dan seterusnya.
Sedangkan pada komputer, bilangan desimal tidak dapat dibaca, yang dapat dibaca hanyalah bilangan biner. Pada komputer, bilangan biner terbesar adalah sebesar 32 digit. Apabila lebih besar dari 32 digit maka bilangan tersebut tidak akan terbaca oleh komputer.
Pada bilangan biner :
Bilangan biner terbesar 1 digit (1) adalah 1.
Bilangan biner terbesar 2 digit (11) adalah 3.
Bilangan biner terbesar 3 digit (111) adalah 7.
dan seterusnya.
Maka, apabila pada komputer bilangan biner terbesar yang terbaca adalah 32 digit maka besarnya adalah (perhitungan dilakukan dengan menggunakan rumus 2^k-1) 4.294.967.295.
Jadi, dapat diambil suatu kesimpulan bahwa untuk memunculkan suatu bilangan random dengan probabilitas perulangan (munculnya bilangan tersebut lagi) sekecil mungkin harus menggunakan ukuran nilai m yang sangat besar (pada komputer maksimal sebesar 32 digit bilangan biner)
ASAL-USUL BILANGAN RANDOM BERDISTRIBUSI UNIFORM (0,1)
Untuk membangkitkan data secara random pada distribusi Uniform (0,1) dapat dilakukan dengan menggunakan rumus seperti di bawah ini :
Where a and m are given positive integers, and where the above means that axn-1 is divided by m and the remainder is taken as the value of xn (Sheldon M.Ross, 2006).
Berdasarkan rumus di atas, maka simulasi untuk membangkitkan data bilangan random dengan distribusi yang lain dapat dilakukan.
Contoh :
1. Membangkitkan data bilangan random berdistribusi Uniform kontinyu x~μ(a,b) dengan menggunakan bahasa pemrograman Pascal adalah sebagai berikut :

2. Membangkitkan data bilangan random berdistribusi Eksponensial dengan menggunakan bahasa pemrograman Pascal adalah sebagai berikut :
Kedua contoh yang dipaparkan di atas dapat pula dilakukan dengan menggunakan bahasa pemrograman yang lain, misal dengan menggunakan software Minitab.
[Penjelasan membangkitkan data dengan menggunakan program Minitab telah dijelaskan pada contoh kedua dalam posting yang sebelumnya dengan judul Contoh Aplikasi Percobaan Simulasi]
Namun, untuk mengetahui apakah hasil bangkitan data dari Minitab benar atau tidak maka tetap diperlukan suatu pengujian. Pengujian ini dapat dilakukan dengan menggunakan Uji Autocorrelation (Otokorelasi).
Pengujian dengan menggunakan Uji Autocorrelation (Otokorelasi) pada program Minitab dilakukan seperti di bawah ini :
1. Membangkitkan data populasi sebanyak 1000 (Calc → Random Data → Uniform dengan lower endpoint (nilai minimum) sebesar 0 dan upper endpoint (nilai maksimum) sebesar 1).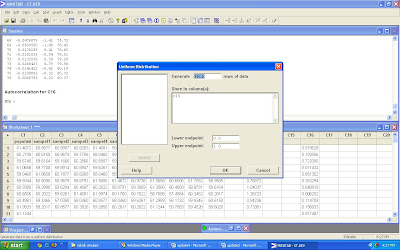
2. Melakukan pengujian dengan menggunakan Uji Autocorrelation ( Stat → Time Series → Autocorrelation)
Hasil akhir dari pengujian Autocorrelation tersebut adalah apabila data yang telah dibangkitkan berada melebihi garis merah maka data tersebut telah acak (random). Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Label: simulasi




.jpg)


