Sabtu, September 12, 2009
Sumber : Buku Ajar Teknik Simulasi (Nur Iriawan)
Model simulasi diskrit digunakan untuk memodelkan suatu sistem yang berevolusi terhadap waktu sedemikian sehingga variabel state sistem hanya berubah nilai pada waktu-waktu tertentu yang banyaknya dapat dihitung. Contoh simulasi diskrit ini adalah antrian. Pada sistem antrian, secara analitis sistem antrian merupakan model yang mempunyai sifat kedatangan pelanggan ke dalam sistem dan kecepatan pelayanannya adalah menuruti distribusi Eksponensial. Sehingga, akan dengan mudah untuk menerapkan persamaan dan solusinya.
[Tambahan informasi : Sistem Antrian juga telah dibahas pada mata kuliah Riset Operasi]
MODEL ANTRIAN
Komponen pada sistem antrian : server (channel), clients (pelanggan), antrian.
Server (channel) : Single server atau Multiple server.
Antrian : Single antrian atau Multi antrian.
Parameter: tingkat distribusi kedatangan, waktu kedatangan, waktu pelayanan, panjang antrian, waktu tunggu, dan utilitas server (waktu sibuk atau total waktu).
Keterangan :
Clients (pelanggan) : individu-individu yang meminta jasa pelayanan.
Server (channel) : individu yang melayani individu yang lain yang meminta jasa pelayanan.
Parameter dalam antrian :
λ : rata-rata tingkat kedatangan.
w : rata-rata panjang antrian.
Tw : rata-rata waktu tunggu.
Ts : rata-rata waktu pelayanan.
Tq : rata-rata waktu yang dihabiskan di dalam sistem (Tw + Ts).
λmax : 1/Ts , tingkat maksimum (secara teori) yang dapat dilayani oleh sistem.
Notasi dalam antrian :
Notasi antrian yang sering digunakan pada sistem antrian satu tahap A/B/C : D/E/F
A menunjukkan sebagai distribusi waktu antar kedatangan.
B menunjukkan sebagai distribusi waktu pelayanan.
C menunjukkan sebagai banyaknya server.
D menunjukkan sebagai disiplin antrian.
E menunjukkan sebagai banyaknya kapasitas antrian.
F menunjukkan sebagai besar ukuran populasi.
Keterangan :
1. A dan B (distribusi kedatangan dan pelayanan pelanggan dalam sistem antrian).
M → Memoryless (Eksponensial / λ).
Er → Erlang (α,β).
G → Arbitrary waktu antar kedatangan.
D → deterministic arrivals or fixed length services.
Contoh : M/M/1 : FIFO/~/~
2. C (banyaknya server).
Menunjukkan banyaknya pelayan yang siap melayani pelanggan yang datang pada sistem antrian. Nilai C>1 menunjukkan bahwa server-server tersebut terpasang parallel.
3. D (disiplin antrian).
Disiplin antrian adalah cara server memilih pelanggan untuk dilayani. Terdapat beberapa pengembangan model dari disiplin antrian sebagai berikut :
(1) FIFO (First In First Out) atau FCFS (First Come First Serve).
Artinya, pelanggan yang pertama datang adalah pelanggan yang akan dilayani pertama kali.
(2) LIFO (Last In First Out) atau LCFS (Last Come First Serve).
Artinya, pelanggan yang terakhir datang adalah pelanggan yang akan dilayani pertama kali. Apabila menggunakan disiplin antrian ini maka akan mengakibatkan terjadinya penumpukan massa atau individu atau dengan kata lain akan tecipta suasana yang kacau.
(3) Random (acak).
Artinya, semua anggota populasi mempunyai peluang yang sama untuk terpilih. Populasi yang dimaksud ini adalah populasi individu yang akan dilayani. Hal yang sama akan terjadi seperti disiplin antrian sebelumnya apabila menggunakan disiplin antrian ini, suasana akan menjadi kacau.
(4) Prioritas.
Artinya, pelanggan yang pertama kali dilayani adalah pelanggan yang mempunyai prioritas terpenting. Hal ini biasanya terjadi pada UGD (Unit Gawat Darurat) pada suatu rumah sakit.
Jika pada suatu kasus, komponen D ini tidak dituliskan berarti disiplin antrian bernilai default (FIFO).
4. E (banyaknya kapasitas maksimum tempat antrian dalam sistem).
Komponen E dapat bernilai :
• Nol, jika tidak ada tempat antri yang disediakan.
• Satu, jika struktur antri hanya memberikan satu tempat antri.
• dst hingga tak terbatas.
Jika pada suatu kasus, komponen E tidak dituliskan berarti tempat antriannya tidak terbatas.
5. F (banyaknya pelanggan yang diijinkan untuk datang ke antrian.
Komponen F dapat bernilai :
• Terbatas, jika hanya pelanggan tertentu saja yang diperbolehkan datang ke dalam antrian.
• Tidak Terbatas, jika semua orang dengan keperluan sesuai tugas server, boleh datang ke antrian.
Jika komponen F ini tidak dituliskan, berarti semua orang dengan keperluan sesuai tugas server boleh datang ke antrian.


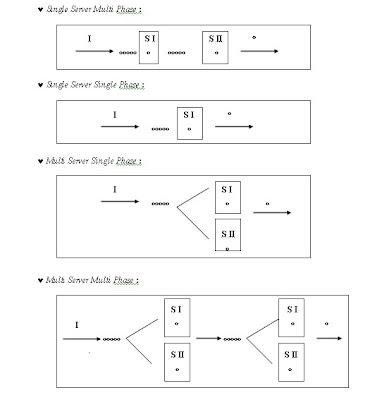
Untuk keterangan lebih lanjut pada sistem antrian server tunggal, dapat dijelaskan dengan menggunakan gambar di bawah ini :

Berdasarkan kasus di atas, terdapat 3 event (kejadian dalam sistem yang dapat mengubah state suatu sistem) :
1. Kedatangan konsumen (arrival) : merupakan event dikarenakan menyebabkan jumlah konsumen yang menunggu bertambah 1 state variabel.
2. Awal pelayanan konsumen : merupakan event dikarenakan menyebabkan status teller berubah dari idle menjadi busy dan jumlah konsumen yang menunggu berkurang 1 state variabel.
3. Kepergian konsumen (departure) : merupakan event dikarenakan menyebabkan status teller berubah dari busy menjadi idle dan jumlah konsumen yang menunggu berkurang 1 state variabel.
Keterangan :
a. Status teller digunakan untuk menentukan apakah konsumen yang baru datang harus menunggu atau bisa langsung dilayani.
b. Banyaknya konsumen yang sedang antri digunakan untuk menentukan apakah status teller setelah melayani konsumen menjadi idle atau tetap busy.
c. Waktu kedatangan tiap konsumen yang antri digunakan untuk menghitung waktu tunggu konsumen.
State Diagram M/M/1
State Diagram M/M/3
SIMULATION CLOCK
Karena model simulasi diskrit bersifat dinamis maka perlu untuk mencatat waktu-waktu tertentu sepanjang simulasi berlangsung dan butuh mekanisme untuk menaikkan waktu simulasi dari suatu nilai ke nilai lainnya. Variabel dalam model simulasi yang mencatat nilai waktu simulasi saat tertentu (current value of simulated time) disebut simulation clock.
Ada dua cara pendekatan yang digunakan untuk memajukan simulation clock, yaitu :
1. Pemajuan waktu berdasarkan event (next event time advance).
Simulation clock pertama kali diberi nilai 0 (nol) dan waktu-waktu terjadinya suatu event di masa mendatang ditetapkan. Nilai simulation clock diubah pada saat suatu event terjadi, setelah itu dilakukan perubahan nilai system state sesuai dengan event yang terjadi dan perubahan waktu terjadinya event berikutnya. Proses perubahan simulation clock dari satu event ke event lainnya berhenti sampe suatu kondisi yang telah ditentukan.
2. Pemajuan waktu dengan jarak tetap (fixed increment time advance).
Kenaikan nilai simulation clock adalah selalu dt (Δt), unit waktu. Setelah dilakukan update simulation clock, dilakukan pengecekan untuk menentukan apakah ada event yang terjadi selama interval waktu sebelumnya. Jika ya maka event yang terjadi dianggap terjadi pada akhir interval waktu, setelah itu system state (statistical counters) disesuaikan.
Metode pendekatan yang pertama lebih mudah dan lebih banyak digunakan pada mayoritas desain bahasa simulasi dan karena metoda yang kedua mempunyai banyak kelemahan. Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Untuk mendownload file yang sudah diposting ini (versi doc) download pada BLOG's CONTENT (klik sesuai judul posting yang ingin di download).
Label: simulasi




.jpg)


